Recently I was playing with Mahout and public weather dataset. In this post I will describe how I used Mahout library and weather statistics to fill missing gaps in weather measurements and how I managed to locate steep mountains in US with a little Machine Learning (n.b. we are looking for people with Machine Learning or Data Mining backgrounds – see our jobs).
The idea was to just play and learn something, so the effort I did and the decisions chosen along with the approaches should not be considered as a research or serious thoughts by any means. In fact, things done during this effort may appear too simple and straightforward to some. Read on if you want to learn about the fun stuff you can do with Mahout!
Tools & Data
The data and tools used during this effort are: Apache Mahout project and public weather statistics dataset. Mahout is a machine learning library which provided a handful of machine learning tools. During this effort I used just small piece of this big pie. The public weather dataset is a collection of daily weather measurements (temperature, wind speed, humidity, pressure, &c.) from 9000+ weather stations around the world.
Artificial Problems
The problems I decided to attack (I made up them by myself, just to set some goals, no serious research was intended) were
- using Mahout’s recommendation tools to fill the missing data points in weather statistics data
- using Mahout’s “similarity tools” to locate nature’s relief influencers on the weather conditions, like mountains, based on weather statistics data
First would allow to fill in gaps in measurements on some of the weather stations. In the second problem the system would locate physical nature’s barriers and other influencers on the weather. By comparing the findings with the physical map one could judge e.g. about which mountains can isolate weather spreading to certain areas. Please forgive me if I use the wrong terms, but I really find the outcome quite interesting. Read on!
Using Recommendation Engine to Fill Missing Weather Measurements
The core (simple) idea is to use recommendation engine to fill in missing measurements. I used User-based recommendation specifically by treating station as a user, date as an item and the temperature as a preference. I know, many can say this isn’t a good way to approach the problem, but for my purpose of learning this worked well.
The Data
The dataset contains 18 surface meteorological elements, from which I selected just few items to be used. So, I chose to work only with temperature to simplify things, though I understood that it could not be enough to reach any interesting result. Moreover, one would argue that it makes much more sense to use precipitation to locate such objects as mountains which affect them a lot. I chose a simpler path, though with quite a big risk of getting nothing. In order to have ability to iterate fast I also used just 2 years of data of the stations located in US. I actually tried to use only California’s station, but this didn’t work well (at least in the beginning before I get to tuning the system logic). For this first problem I didn’t use any of the stations location and altitude information to get things more interesting.
To evaluate the system I simply divided the dataset into two pieces and used one of each as training sample and another one as evaluation sample. Please see the code below.
Data Cleaning
I had to clean some the data before I could use it for training the recommender. It seems like there were some stations which has different IDs but has same location in the dataset. I cleaned them to have only one station in the same place to avoid increased weighting of the same station. I also cleaned Alaska’s stations and most of those which are not on the continental area as they are usually alone standing and do not have related weather conditions to others and only bring the noise for the recommender.
Preparing Input Data for Mahout
So, in our interpretation stations are users and days (dates) with temperature are items with user preference, but there’s more to that. It makes sense to try to use connection between dates which is just dropped by this simple interpretation: dates may stand close to each other or be far from each other; by comparing the change of the temperature during some period helps to judge about “weather closeness” of two stations. To make use of that for calculating similarity I also added <date, diff with the N days ago> pairs. E.g. for input:
20060101,56 20060102,61 20060103,62
I got these preferences:
20060101_0,56 20060102_0,61 20060102_1,+5/1 20060103_0,62 20060103_1,+1/1 20060103_2,+6/2
I divided the difference with the further standing “N day ago” by N so that they are weighted less. Otherwise difference between far from each other days going to be bigger than from than that from close days, while it is the close days difference which is more interesting actually. For the same purpose I tested with up to 5 extra pairs (diffs with up to 5 previous days).
Moreover, when it comes to comparing the change it may really not matter by how much temperature was changed, it is enough to know that it was changed at least by some value d (onlyDirectionOfChange=true, changeWeight=d in results below). So, e.g. given value d=2.0, comparing change with previous 2 days (prevDays=2 in the results below) the example data above is going to look like this:
20060101_0,56 20060102_0,61 20060102_1,+2/1 20060103_0,62 20060103_1,0 20060103_2,+2/2
Running Recommender Evaluating Results
Once data is prepared and you know which recommender parameters (including similarities and their parameters and such) training recommender and evaluating the results is very simple. Please find below the code for non-distributed recommendation calculation.
DataModel model = new FileDataModel(statsFile);
RecommenderEvaluator evaluator = new AverageAbsoluteDifferenceRecommenderEvaluator();
RecommenderBuilder builder = new RecommenderBuilder() {
@Override
public Recommender buildRecommender(DataModel model) throws TasteException {
UserSimilarity similarity = new EuclideanDistanceSimilarity(model);
UserNeighborhood neighborhood = new NearestNUserNeighborhood(neighbors, similarity, model);
Recommender recommender = new GenericUserBasedRecommender(model, neighborhood, similarity);
return recommender;
}
};
return evaluator.evaluate(builder, null, model, 0.95, 1.0);The code above shows just one of many possible recommender configurations (and it doesn’t show the fact that we use more data for calculating user similarity as explained in the previous section). Since we really care about the numbers we throw away similarities that don’t take into account the preference value, like TanimotoCoefficientSimilarity. During the (limited) tests I ran it appeared that the simplest EuclideanSimilarity worked best.
Result
My (limited) tests showed the following best results with configurations:
SCORE: 2.03936; neighbors: 2, similarity: {onlyDirectionOfChange=true, changeWeight=2.0, prevDays=1}
SCORE: 2.04010; neighbors: 5, similarity: {onlyDirectionOfChange=true, changeWeight=5.0, prevDays=2}
SCORE: 2.04159; neighbors: 2, similarity: {onlyDirectionOfChange=false, prevDays=1}Where:
- “score” is the recommendation score, i.e. in our case the average absolute difference in recommended value and actual value
- “neighbors” is the number of neighbors used (in NearestNUserNeighborhood) to provide recommendation
- “onlyDirectionOfChange” is whether we use absolute change value when comparing with previous days (value is false) or we comparing with the certain threshold as explained above (value is true)
- “changeWeight” is the threshold to compare the change with
- “prevDays” is the number of previous days to compare with
Using Statistics-based Similarity to Locate Weather Influencers
The core (simple) idea is to calculate similarity between stations based on weather statistics and compare it with the physical distance between the stations: if there’s a great difference then assume that there’s something in between such stations that makes the weather noticeably different. Then, the only things we need to define is:
- how to calculate similarity
- haw to calculate physical distance
- what is a *noticeable* difference between weather stats based similarity and physical distance
- where is this “in between” located
The plan was to use Mahout’s user similarities to calculate the distance between stations based on weather statistics data (taking it as user preferences similar to the first part) and compare it with the physical distance. The evaluation of the results is not very well automated as in previous part, though it could be have I more time for this. To evaluate I just plotted the results and compared this image with the physical map of US.
The Data
The data was used the same as was used in the first part plus physical location of the station, which was used to calculate physical distance between them.
Data Cleaning
Data cleaning had the same logic as for the first part. Though I did more severe cleaning of stations not on the continent and near the shore: we all know that ocean influences the weather a lot, so if I didn’t do that, all shore points would have been considered to be “outliers”. Actually, not only ocean shore-close stations, but most of those near the border of US were removed for the sake of removal algorithm simplicity.
Preparing Input Data for Mahout
The input data were prepared the same way as in first part, the “user preferences” contained <station, temperature> pairs and added <date, diff with the N days ago> pairs. Note, that there are a lot of ways to calculate distance between stations using weather stats, I simply chose the one which would allow me to re-use the same prepared data files from the first part of experiment.
Running the Implementation & Evaluating Results
Let’s have a closer look at how each item from the list in idea overview section was defined.
How to calculate similarity?
As mentioned above I chose simple (similar to the first part) similarity calculation. Simple EuclideanDistanceSimilarity worked well.
How to calculate physical distance?
Physical distance was calculated as Euclidean distance between stations using latitude, longitude and altitude. The longitude was given a much greater weight, because the temperature tends to be affected a lot by longitude coordinate: the further South you go (in Northern Hemisphere where US is) the lower the temperature without any physical relief influencers. Also altitude was given a stronger weight because it has the same strong affect on the temperature.
And, of course to make distance comparable with calculated similarity we need it to be in 0..1 range (with the value close to 1 showing the smallest distance). Hence distance was calculated as 1 / (1 + phys_dist(station1, station2)).
What is a *noticeable* difference between weather stats based similarity and physical distance?
I assumed that there’s an exponential dependency between calculated physical distance of the two stations and similarity calculated from weather stats. I found an average growth rate (of the similarity given the physical distance) using all stations pairs (remember that we have not huge amount of stations, so we can afford that) and used it to detect those pairs that had much greater difference between their physical distance and similarity calculated from weather stats.
Where is this “in between” located?
For those “outlier” pairs detected I put single “physical influencer” point on the map which location is exactly the middle point between those stations (unweighted latitude and longitude were used to calculate it).
Result
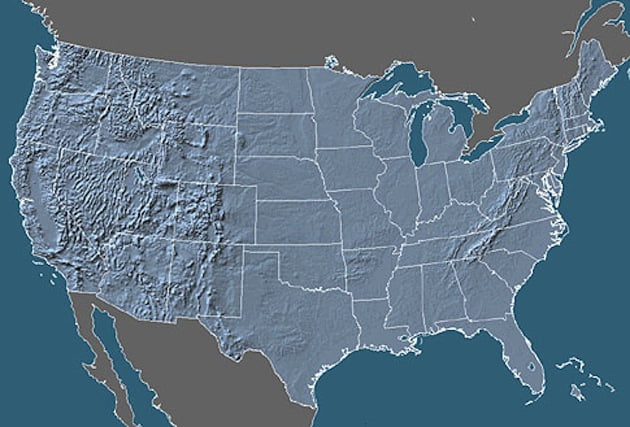
Result is better represented and evaluated by comparing the following two images: first created by our system and second being a physical map of US.
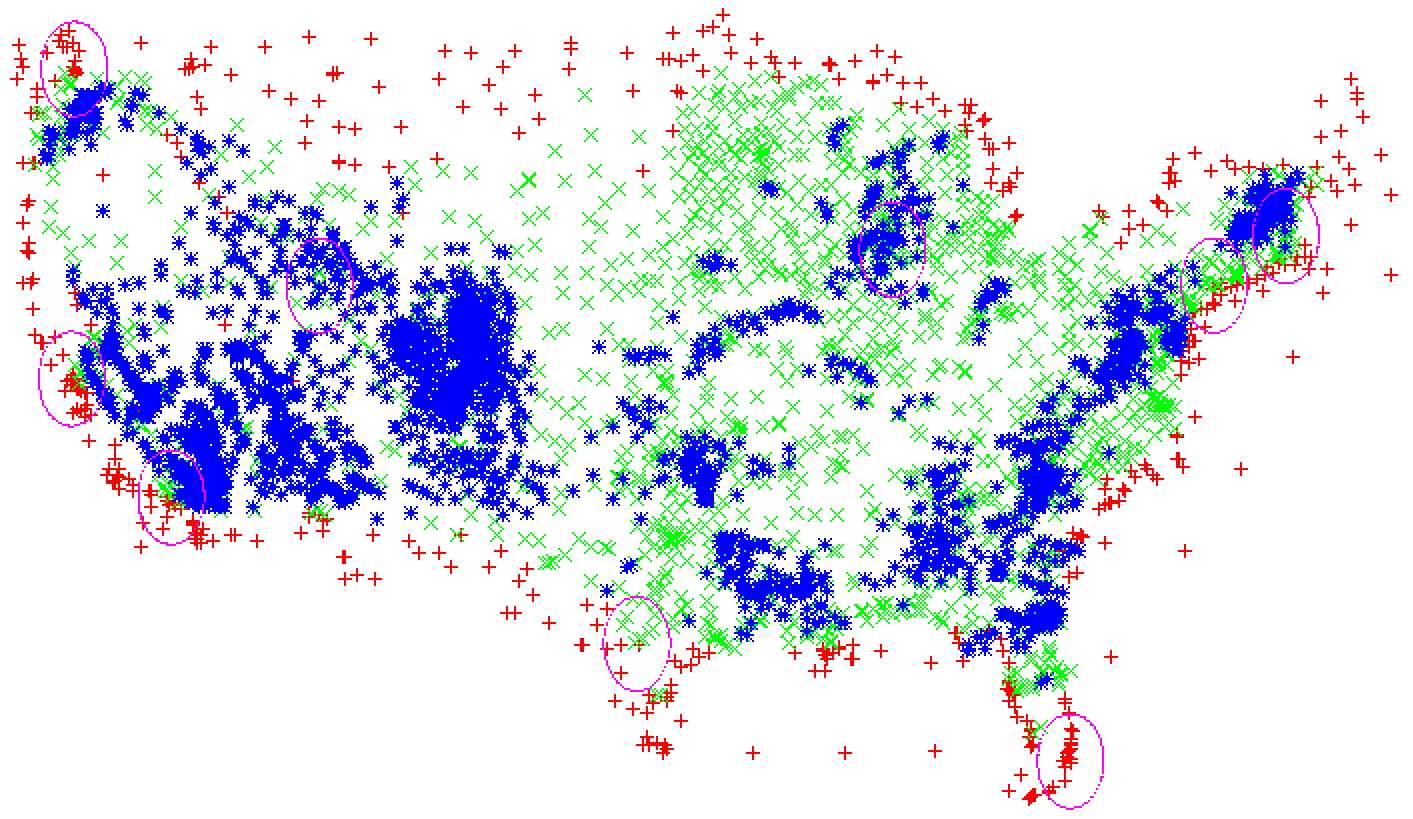
green – stations which stats were used
blue – found weather “influencers”
circles – some of the cities (Seattle, San-Francisco, Los-Angeles, San-Antonio, Salt Lake City, Miami, New York City, Boston, Chicago)
Compare with:
Note how steep mountains are there in the first image. Of course, there’s noise from lakes, gulfs and other sources. But look how well it drew the relief of California!
What Else?
There are a number of things that can be done to obtain even more interesting results. Just to name a few:
* use not only temperature but other measures, e.g. precipitation as noted in the beginning of the post
* show influencers with different color (heat map) depending on how they affect the weather
* and more
Summary
I touched only a very small piece of the great collection of machine learning tools offered by Mahout and yet managed to get very interesting (and useful?) results. I also used just a small part of the public weather dataset available to everyone and yet it was enough to get meaningful outcome. And there are so many different public datasets available online! There’s so much exciting things one can do with such a powerful tool like Mahout and a pile of data.